文|新智元

编辑|大明

麻省理工学院的科学家成功地打造出了能够变形成人脸的神奇材料。

3D打印中的下一个重要突破，可能就是利用同样的制造技术制造“ 4D材料”，这种材料可以随着时间的推移而变形，以响应周围环境的变化（比如湿度和温度）。它们有时也被称为“主动折叠”或“变形材料”系统。

此前的研究已经成功实现了让此类材料变形为简单结构。麻省理工学院机械工程师Wim van Rees 团队设计了一种理论方法，可以将薄平板材料变形为更复杂的形状，如球体，圆顶，甚至人脸。

Wim van Rees表示：“我的思路是从复杂的3D形状开始，比如人脸一样，然后问：'我们如何对材料进行编程，来实现这个目标？这实际上是个‘逆设计’问题。”

他最初的模拟实验对象是理想材料，材料的膨胀或收缩能力是无限的。但是，大多数现实世界中的材料其实都存在。这就是19世纪数学家卡尔·弗里德里希·高斯（Carl Friedrich Gauss）首次提出的“双曲率”问题。

卡尔·弗里德里希·高斯

1828年，高斯提出了“绝妙定理”（Theorema Egregium）。该定理指出，只要测量曲面表面的角度和距离，就可以确定其高斯曲率。也就是说，对曲面进行弯曲时，其表面高斯曲率不会改变。

绝妙定理是微分几何中关于曲面的曲率的重要定理，这定理说曲面的高斯曲率可以从曲面上的长度和角度的测量完全决定，无需理会曲面如何嵌入三维空间内。换言之，高斯曲率是曲面的内蕴不变量。用现代术语可表述为：

高斯曲率在局部等距变换下不变。

不过有个问题：平面无法拉伸，收缩或撕裂，如果要想将平板变形为具有不同高斯曲率的复杂形状时会遇到问题。Van Rees将这个问题比作“包足球”的挑战。纸的高斯曲率为零，而球的曲率为双。因此，为了用纸包把足球包上，必须在侧面和底部把纸弄皱，纸必须在所有合适的位置实现伸展或收缩。

为了解决这个问题，van Rees团队使用网状的网格结构，而不是在最初的模拟中建模生成连续的纸张。他们用橡胶材料制成晶格，当温度升高时，该材料会膨胀。晶格中的间隙使材料更容易适应其表面积剧烈变化。

麻省理工学院的团队使用高斯图像创建了一个虚拟地图，该地图显示了要重新将材料变形为人的面部需要将平面弯曲多少。然后，研究人员设计了一种算法，将设计方案转换为晶格中正确的骨骼（rib）模式。

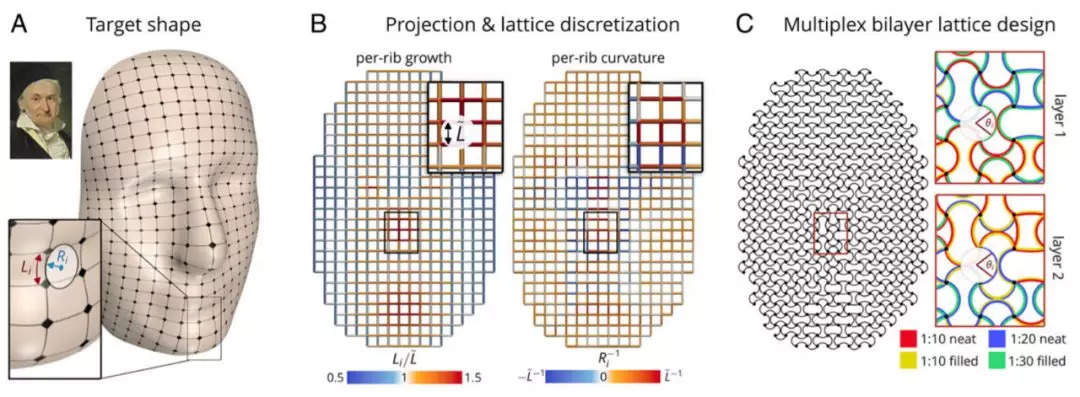
这些特定模式的rib在整个网格片上以不同的速率生长，每个rib都可以弯曲成鼻子或眼窝的形状。印刷之后的网格在热烘箱中固化，然后在盐水浴中冷却至室温。瞧！人脸诞生了！

研究人员还做了一个包含导电液态金属的晶格，相当于有源天线，其共振频率可以随着人脸的变形而变化。

这些形变材料可能被用来制造仅改变温度（或其他环境条件）就能自行展开和膨胀的帐篷。此外还可能制造可变形的望远镜镜片、支架，用于人造组织的支架和软体机器人等等。

范·里斯说：“比如我现在希望将这种材料结合到机器人水母中，让机器人水母可以变形实现游泳。也可以将其用作执行器，例如人造肌肉，就可以生成任意形状的肌肉，也可以为软体机器人领域的设计打开一片天地。”

参考来源：dailymail